拉普拉斯变换概念
Fourier变换的局限性
当函数f(t)满足Dirichlet条件,且在$(-\infty,+\infty)$上绝对可积时,便可以进行古典意义下的Fourier变换,同时由于绝对可积是一个非常强的条件,使得一些简单的函数,如常数函数、线性函数、正弦函数、余弦函数等等的Fourier变换也受到限制。
同时在实际的工程实践中,许多信号实际上在t<0是根本不存在或者没有意义,于是不可能对其做谷古典意义上的Fourier变换。这就是拉普拉斯变换的由来。
拉普拉斯变换
拉普拉斯变换的引入
- 将函数f(t)乘一个单位阶跃函数u(t),使得函数在t<0的部分补0;
- 将函数再乘上一个指数衰减函数$e^{-\beta t}(\beta > 0)$,使得函数再t>0的部分尽快地衰减下来。
这样就在一定程度上使得函数可能满足Fourier函数的变换条件,从而对齐进行Fourier变换。

拉普拉斯变换的定义
设函数f(t)是定义在$(0,+\infty)$上的实值函数,如果对于复参数$s=\beta+jw$,积分$F(s) = \int_{0}^{+\infty}f(t)e^{-st}dt$在复平面s的某一区域内收敛,则称F(s)为f(t)的拉普拉斯变换或者像函数,记为:
也就是:
相应地,称f(t)为F(s)的拉普拉斯逆变换或者像原函数,记为:
事实上,f(t)的拉普拉斯变换也就是$f(t)u(t)e^{-\beta t}$的傅里叶变换。
拉普拉斯变换的存在性定理

事实上也就是说在大部分情况下,当某个函数的增长速度比指数函数慢的时候,其拉普拉斯变换就存在。
拉普拉斯变换的性质
再下面给出的Laplace变换的性质中,所涉及到的函数的Laplace变换均假定存在,他们的增长指数均假定为C。并记:
对于涉及到的一些运算,如求导、积分、极限以及求和等的次序交换问题均不另作说明。
线性性质与相似变换
容易证明拉普拉斯变换具有线性性质:
也容易证明拉普拉斯变换具有相似性质,其证明如下:

延迟性质与位移性质
拉普拉斯变换的延迟性质如下:

需要注意的是此时再延迟性质中专门强调了当t<0时,f(t) = 0 这一约定。由此本性质也可以表示为:
可见再使用此性质求解其逆变换时:
微分性质
导数的象函数
具体证明过程如下:
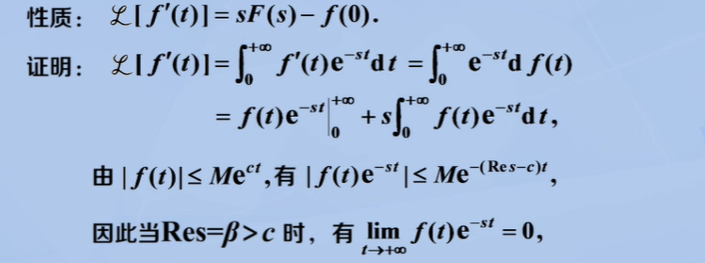
更一般地有如下结论(实际上,此结论的证明和一阶导数情况的证明一致)
其中$f^{k}(0)$应该理解为,$\lim_{t \to 0^{+}}f^{k}(t)$.拉普拉斯这个性质可以用于求解微分方程和微分方程组的初值问题。
象函数的导数

积分性质
拉普拉斯变换的积分性质同样可以分为两类,第一类是应该函数的象函数与它积分之后的象函数的关系。第二类是像函数的原函数与它积分之后的关系。也就是和其微分性质一样,一类是先求积分后做变换,一类是先做变换后求积分。
积分的象函数
积分的象函数性质如下:
证明过程如下:

同理可知,若先做n此变上限积分后能够得到:
象函数的积分

拉普拉斯变换中的卷积与卷积定理
卷积的定义

显然上述式子满足交换律,结合律,分配律等式子。
卷积定理
上述定理的证明过程与傅里叶中的卷积定理可知。
拉普拉斯逆变换
对于拉普拉斯逆变换,有如下公式可以求解其具体形式,我们称之为反演积分公式——Laplace逆变换公式。
公式推导
- 首先由拉普拉斯变换和傅里叶变换的关系可以知道,函数f(t)的拉普拉斯变换$F(s) = F(\beta + jw)$就是函数$f(t)u(t)e^{-\beta t}$的Fourier变换。
- 而后再依据Fourier逆变换,在f(t)的连续点t处,有:
- 将上式两边同乘$e^{\beta t}$,并由$s = \beta + jw$,有:
于是得到:
反演积分公式
于是通过上述推导,我们得到了如下反演积分公式:

留数法计算反演积分
假设函数F(s)除在半平面$Res \leq c$内有有限个孤立奇点:$s_{1}, s_{2}, s_{3}, … ,s_{n}$外是解析的,且当$s \to \infty$时,$F(s) \to 0$,则:

查表法计算反演积分
利用拉普拉斯的变换性质,依据一些已知函数的拉普拉斯变换来求逆变换,大多数情况下,象函数F(s)常常为分式的形式$F(s) = \frac{P(s)}{Q(s)}$,那么容易知道$P(s)$和$Q(s)$是实系数多项式,由于真分式容易进行因式分解,所以利用查表法也是一种较为方便的方法。

拉普拉斯变换的应用
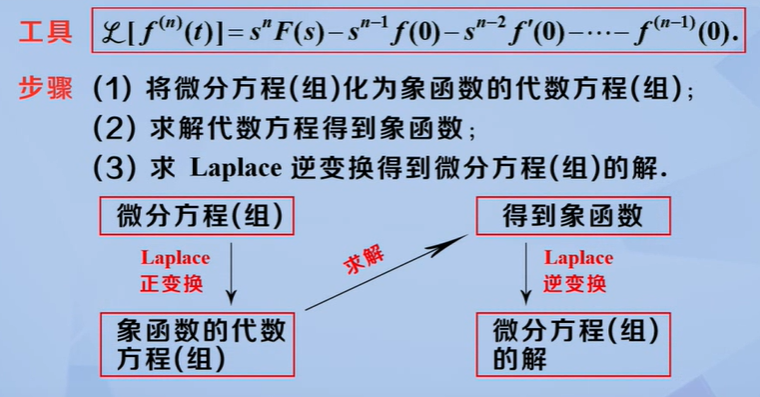
求解常微分方程(组)
拉普拉斯变换是求解常微分方程的重要工具,其能够将常微分方程(组)化为象函数的代数方程(组)。而后通过求解象函数得到代数方程,最后再通过拉普拉斯逆变换得到原微分方程(组)的解。