信号与系统--第二章--系统的时域分析

时域分析方法概述

时域对系统的描述通过微分方程与差分方程对其进行描述。其中对于输入与输出变量，通常通过医院n阶微分方程来描述，对于引入状态变量的情况则可以通过n元一阶微分方程描述。

时域的分析方法不涉及任何变换，直接求解系统中微分方程以及差分方程，这种方法比较直观，涉及的物理概念比较清晰。

本章主要解决以下两个问题：其一式系统变复杂了（微分方程阶次变高），应该如何处理？第二个问题式信号变复杂了，应该如何处理。

线性时不变系统的描述

一个 线性时不变系统 ，其激励信号与响应信号之间的关系可以通过下列形式来描述：

$$\boldsymbol{a}_{\boldsymbol{n}}\frac{\boldsymbol{d}^{\boldsymbol{n}}\boldsymbol{r}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}^{\boldsymbol{n}}}+\boldsymbol{a}_{\boldsymbol{n}-1}\frac{\boldsymbol{d}^{\boldsymbol{n}-1}\boldsymbol{r}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}^{\boldsymbol{n}-1}}+\cdots \boldsymbol{a}_1\frac{\boldsymbol{dr}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}}+\boldsymbol{a}_0\boldsymbol{r}\left( \boldsymbol{t} \right) \\ =\,\,\boldsymbol{b}_{\boldsymbol{m}}\frac{\boldsymbol{d}^{\boldsymbol{m}}\boldsymbol{e}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}^{\boldsymbol{m}}}+\boldsymbol{b}_{\boldsymbol{m}-1}\frac{\boldsymbol{d}^{\boldsymbol{m}-1}\boldsymbol{e}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}^{\boldsymbol{m}-1}}+\cdots \boldsymbol{b}_1\frac{\boldsymbol{de}\left( \boldsymbol{t} \right)}{\boldsymbol{dt}}+\boldsymbol{b}_0\boldsymbol{e}\left( \boldsymbol{t} \right)$$

上述微分方程右端只含有激励，左端只含有响应，且其中$a_{i},b_{i}$均为常数。阶次通过n,m中最高次的项数来判定。

对于此类型的微分方程，其求解方法可以归纳为下表：

经典法

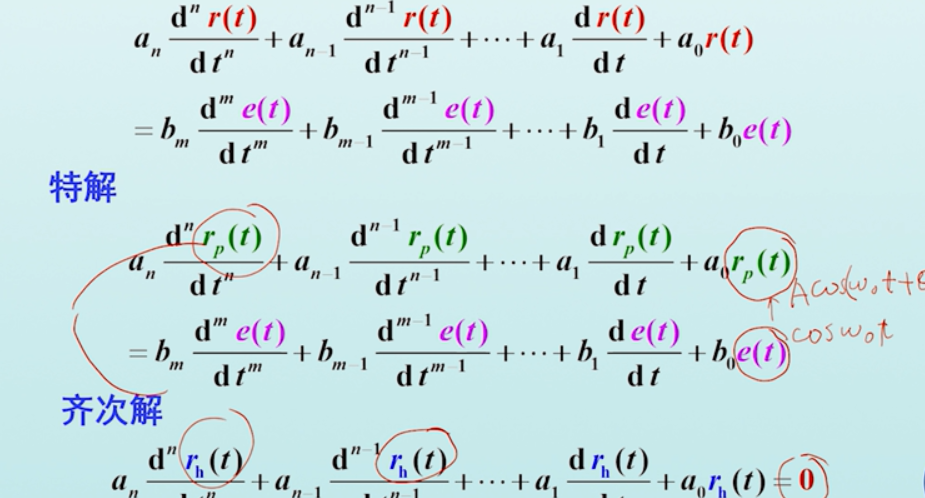
求解方法按照高等数学中学习的求解齐次方程即可。

起始点的跳变与冲激函数

跳变的定义如下：

电路系统中，状态代表了储能元件的储能情况。

冲击函数匹配法确定系统初始条件

首先我们介绍配平的原理，在t=0时刻，微分方程左右两端的$\delta (t)$及其各界导数应该平衡（其他项也应该平衡，我们讨论初始条件的时候可以不考虑其他项。）

$$\Delta u(t)$$

表示从$0_{-}$到$0_{+}$的相对单位跳变函数。

响应的划分

零输入响应+零状态响应

概念

零输入响应指的是没有外加激励信号，只由其实状态所产生的响应称为零输入响应；零状态响应指的的其实状态等于零由外加激励信号产生的响应。

零输入响应

1. 输入为：0，
2. 方程类型为：齐次方程
3. 解的形式为：特解为0，仅有齐次解
4. 边界条件为不跳变

零状态响应

1. 零状态：$r_{zs}(0_{-})=r_{zs}^{‘}(0_{-})=\dots=r_{zs}^{n-1}(0_{-})=0$
2. 输入：给定的输入
3. 方程：原方程
4. 解的形式：特解+齐次解
5. 跳变：会发生跳变，求解繁琐，故引出卷积积分法。

自由响应+强迫响应

自由响应由系统本身的特性决定，与外加的激励形式无关，对应于齐次解，系统的特征根也被称为“自然频率”和“自由频率”。强迫响应是指去觉悟外加激励的响应形式，其对应于特解。

暂态响应+稳态响应

暂态响应指的是当$t \to +\infty$时候趋于0的项，稳态响应指的是当$t \to +\infty$时，保留下来的分量。

对线性系统的进一步认识

1. 响应可分解：零输入响应+零状态响应
2. 零输入线性：当激励为零时，系统零输入响应对于各其实状态呈线性。
3. 零状态响应：当其实状态为零时，系统的零状态响应对于各激励信号呈线性。

利用冲击响应与阶跃响应描述线性时不变系统

冲击响应和阶跃响应的定义

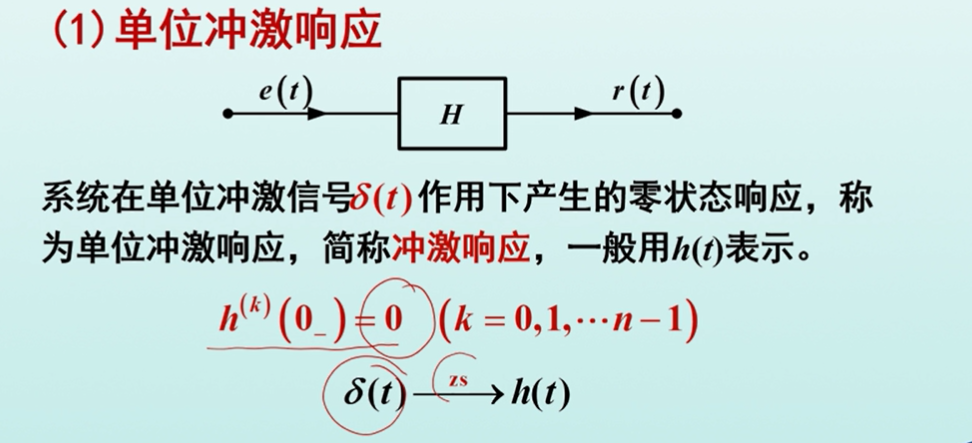
单位冲击响应

系统再单位冲击信号$\delta (t)$的作用下产生零状态响应，称为单位冲击响应，一般用h(t)表示。

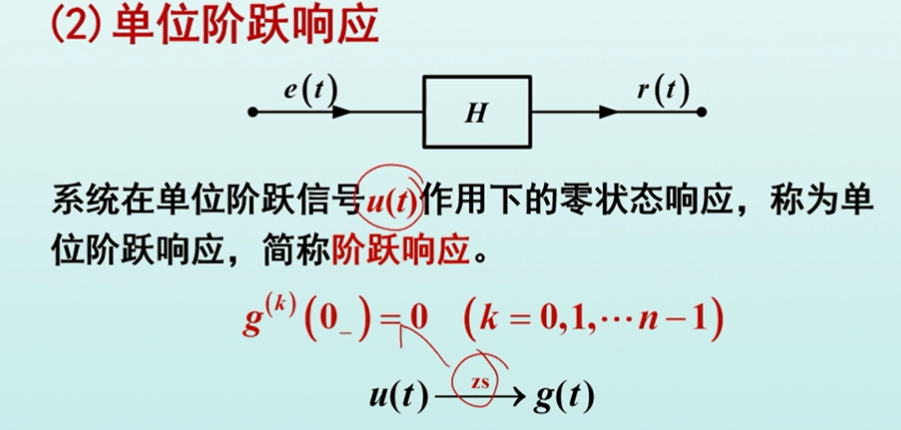
单位阶跃响应

单位阶跃响应指的是系统再单位阶跃信号作用下得到的零状态响应，称为单位阶跃响应，简称阶跃响应。

典型系统的单位冲击响应与单位阶跃响应

标量乘法器

标量乘法器的输出与输入之间的关系为：$r(t) = ae(t)$,那么容易得到输入信号为单位冲击响应$\delat(t)$的时候，输出为：$h(t) = a\delta(t)$.

微分器

微分器的输出与输入之间的关系为：$r(t) = \frac{de(t)}{dt}$,那么容易得到输入信号为单位冲击响应$\delat(t)$的时候，输出为：$h(t) = \frac{d\delta(t)}{dt}$.

积分器

积分器中的积分是关于时间t的一个变上限积分，$r(t) = \int_{-\infty}^{t}e(\tau)d\tau$，将输入信号代入$\delta(t)$之后，我们得到：$h(t) = \int_{-\infty}^{t}\delta(\tau)d\tau =u(t)$.事实上单位冲击的积分就是单位阶跃函数。

延时器

延时器是对输入信号做时间的延迟$r(t) = e(t-\tau)$,输入信号变为单位冲击信号后有:$h(t) = \delta(t - \tau)$.

因果系统中利用微分方程求解冲击响应

主要有以下几种方法求解：

1. 奇异函数相平衡法，确定解的形式，也就是包含哪些函数项，而后求其待定系数。
2. 经典法，只有齐次解的情况，通过跳变找回起义函数及其导函数项。
3. 齐次解法，利用线性时不变系统的性质。
4. 拉普拉斯变换

单位冲击响应的求解

1. t<0,零状态，h(t)=0
2. t>0,齐次解,$h(t) = \sum_{i=1}^{n}A_{i}e^{a_{i}t}$
3. t=0,可能包含冲击函数及其导函数项

容易看出，对于上述方程而言，其右侧单位冲击信号的最高阶导数项数，一定在左侧单位冲击响应的最高阶导数项中。下面我们对其做具体分析：

1. n>m

1. n=m

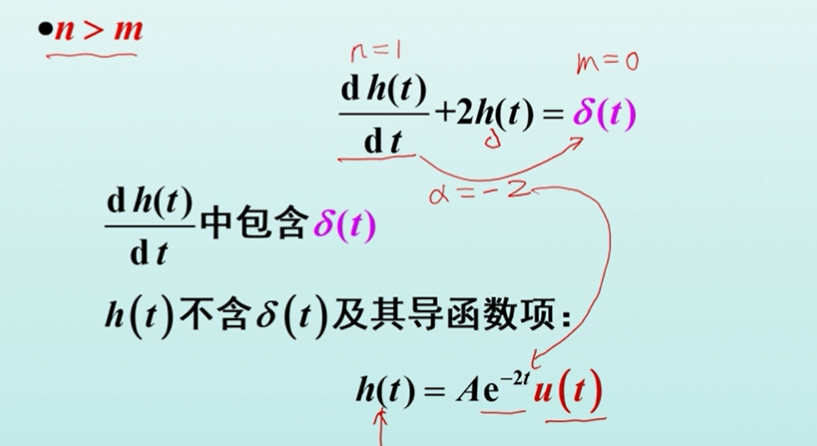
1. n $<$ m

而后利用奇异函数相平衡即可求得待定系数。

单位阶跃响应的求解

对于单位阶跃信号的求解，主要有以下两种方法：

1. 系统的输入$e(t) = u(t)$,其响应为$r(t) = g(t)$.系统方程的右端将包含阶跃函数$u(t)$及其导函数项，所以除了齐次解外，还有特解项。
2. 也可以依据线性时不变系统特性，利用冲击响应与阶跃响应关系求解阶跃响应。

讨论利用冲击响应判断系统的因果性和稳定性

因果系统的单位冲击响应满足如下特性：

$$h(t) = 0 (t < 0)$$

而因果信号就可以定义为：若某信号满足如下形式，则称其为因果信号

$$x(t) = 0 (t<0)$$

而稳定系统的因果信号要满足如下性质：

$$\int_{-\infty}^{+\infty}|h(t)|dt < \infty$$

也就是说稳定系统在单位冲击响应的作用下需要满足绝对可积性质。

卷积

卷积的引出

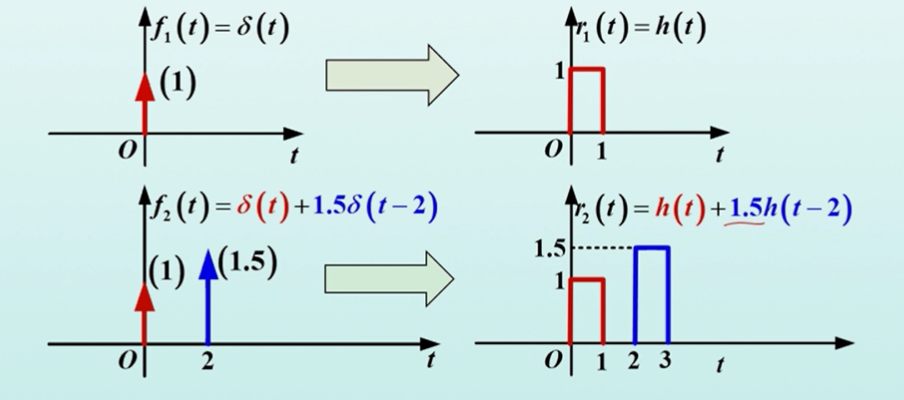
卷积的思想来源于单位抽样信号对原信号的分解作用，对于某一信号，为了将其分解，我们利用微积分的思想，将其划分为矩形的小区间，于是得到如下结果：

而后对上述式子做一个变形，得到：

$$e(t) \approx \sum_{\tau = -\infty}^{+\infty}e(\tau)\frac{u(t-\tau)-u(t-\tau-\Delta\tau)}{\Delta \tau}\tau$$

上式两侧取极限，得到积分的定义：

$$e(t) = \int_{-\infty}^{+\infty}e(\tau)\Delta(t - \tau)d\tau$$

于是我们就将任意信号表示为了时移的单位冲击信号的加权叠加。

利用卷积求零状态响应

同理若，将此卷积信号作为激励加载在某一系统两侧，得到：

卷积的定义

于是得到卷积的定义：
设有两个函数$f_{1}(t)$和$f_{2}(t)$,积分：

$$f(t) = \int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)d\tau$$

称此时的f(t)为$f_{1}(t)$与$f_{2}(t)$的卷积积分，简称卷积，记为：

$$f(t) = f_{1}(t)\otimes f_{2}(t) \\ f(t) = f_{1}(t) * f_{2}(t)$$

卷积的计算

由于系统的因果性或者激励信号存在时间的局限性，容易知道，卷积的积分限会有变化。卷积积分中的积分限的确定是卷积积分计算的关键。接下来对于各种卷积的计算方法，我们注意做一个说明：

解析式法

解析式法使用纯数学的方法进行推理得到。若其中不含有奇异函数则只需要按照微积分中不定积分计算即可，若其中含有奇异函数，则需要对奇异函数的取值范围做进一步讨论。从而确定积分的上下限。接下来我们给出一个例子:

例1：已知$e(t) = u(t) - u(t-t_{0})$, $h(t) = e^{-t}u(t)$, 求$r(t) = e(t)*h(t)$,设$t>0$.

解：
首先我们写出此时两个函数做卷积的表达式：

$$\begin{split} & r(t) = \int_{-\infty}^{+\infty}e(\tau)h(t-\tau)d\tau \\ & \qquad = [u(\tau) - u(\tau - t_{0})]e^{-(t-\tau)}u(t-\tau)d\tau \\ & \qquad = e^{-t}\int_{-\infty}^{\infty}e^{\tau}[u(\tau)u(t-\tau)]d\tau - e^{-t}\int_{-\infty}^{\infty}e^{\tau}[u(\tau-t_{0})u(t-\tau)]d\tau & \qquad = r_{1}(t) - r_{2}(t) \end{split}$$

于是此时我们的问题转化为求解$r_{1}(t),r_{2}(t$.那么我们分别对齐分析，得到：

$$r_{1}(t) = e^{-t}\int_{-\infty}^{\infty}e^{\tau}[u(\tau)u(t-\tau)]d\tau$$

分析其中的奇异函数，我们可以得到t和$\tau$的取值范围：
$\tau > 0, t-\tau >0 \to 0 < \tau 0$,也就是t的取值不是任意的，而是对于t有一定约束的。于是我们不难得到此时的结果:

$$r_{1}(t) = [e^{-t}\int_{0}^{t}e^{\tau}d\tau]u(t) = (1-e^{-t})u(t)$$

第二部分$r_{2}(t)$的求解同理可知，对于$r_{2}(t) = e^{-t}\int_{-\infty}^{\infty}e^{\tau}[u(\tau - t_{0})u(t-\tau)]d\tau$.对其中阶跃函数取值进一步分析得到如下约束条件：

$$\tau - t_{0}>0 \\ t-\tau >0$$

也就是：$t_{0}<\taut_{0}$,于是在对积分变限之后得到：

$$r_{2}(t) = [e^{-t}\int_{t_{0}}^{t}e^{\tau}d\tau]u(t-t_{0})$$

于是$r_{1}(t) - r_{2}(t)$就得到：$r(t) = -[1-e^{-(t-t_{0})}]u(t-t_{0})$

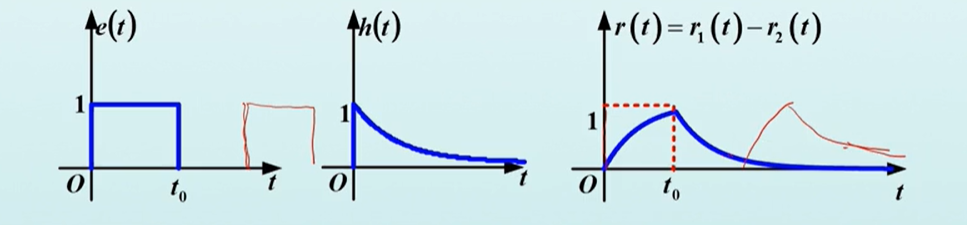
图解法

对于函数解析式较为复杂的情况，利用图解法可以直观地确定积分限。

$$g(t) = \int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)$$

所谓图解法的精髓在于利用信号的变换关系改变函数的形态，而将其中某一个函数变化为区间关于t的函数，而后移动此函数。从而方便我们对t作分段讨论。也就是利用图解法时，其总共有如下几个步骤：

1. $f_{1}(t) \to f_{1}(\tau)$,积分变量改为$\tau$
2. $f_{2}(t) \to f_{2}(\tau)$,将其作倒置变换和时延变换$f_{2}(t-\tau)$.
3. 将二者相乘，$f_{1}(\tau)f_{2}(t-\tau)$.
4. 乘积的积分： $\int_{-\infty}^{+\infty}f_{1}(\tau)f_{2}(t-\tau)$.

连续卷积的性质

代数性质

1. 交换律

交换律的数学表述如下：$f_{1}f_{2} = f_{2}f_{1}$

1. 分配律

分配律的数学表述如下：$f_{1}(t)*[f_{2}(t)+f_{3}(t)]=f_{1}(t)f_{2}(t)+f_{1}(t)f_{3}(t)$.

分配律意味着系统并联，$h(t) = h_{1}(t)+h_{2}(t)$

1. 卷积的结合律

卷积的结合律数学表述如下,$f(t)h_{1}(t)h_{2}(t)=f(t)[h_{1}(t)h_{2}(t)]$.

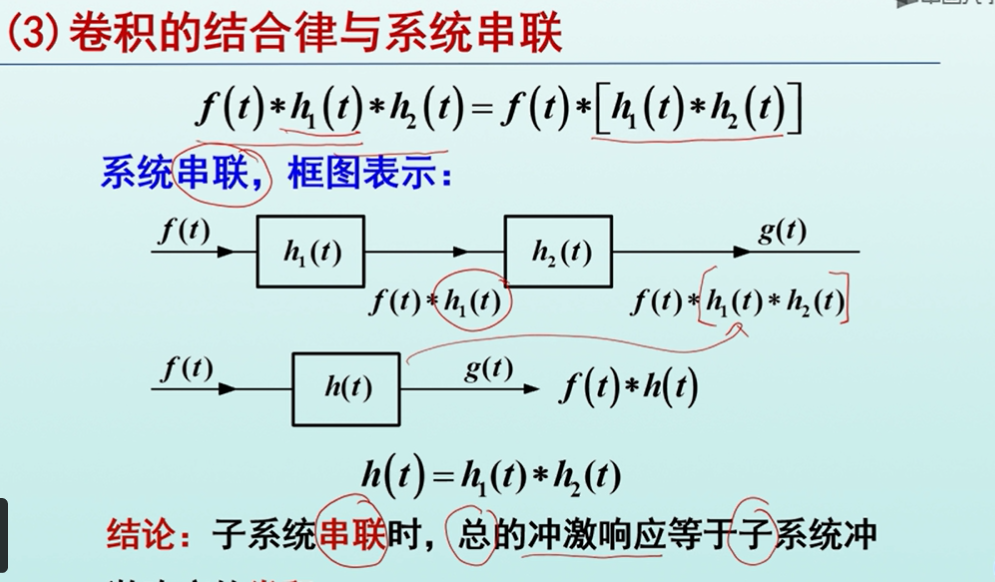
结合律意味着系统级联：$h(t) = h_{1}(t)*h_{2}(t)$

卷积的时移性质

若$f(t) = f_{1}(t)f_{2}(t)$，则$f_{1}(t-t_{1})f_{2}(t) = f(t-t_{1})$.

与奇异函数的卷积

与冲击函数的卷积

利用抽样性质，我们容易知道，在与冲激函数卷积后得到原函数。
$f(t) * \delta(t) = \int_{-\infty}^{+\infty}f(t-\tau)\delta(\tau) d\tau=f(t)\int_{-\infty}^{+\infty}\delta(\tau)d\tau=f(t)$.

同时通过时延性质，我们容易知道，若此时将冲击函数改为$\delta(t-t_{0})$，我们容易得到$h(t) = \delta(t-t_{0})$.

若与冲击偶函数进行卷积，那么容易得到此时事实上就是经过一个微分器：
$f(t) \delta’(t) = f’(t)$
同理，对于$\delta^{k}(t)$容易知道:$f(t)\delta^{(k)}(t)=f^{(k)}(t)$.

若此时有时延,是的此时$\delta(t)$变为$\delta(t-t_{0})$,那么得到的结果也要相应地延迟。

与阶跃函数的卷积

显然知道，与阶跃函数所作卷积相当于一个积分器也就是说：

$$f(t) * u(t) = \int_{-\infty}^{+\infty}f(k)dk$$

卷积的微分与积分性质

微分性质

差分方程与离散时间系统

差分方程的求解

迭代法

迭代法是目前差分方程常用的一种方法，差分方程本质上就是迭代的等式。例如：

但是这种方法很难得到解析解。

时域经典法

齐次解

$$y(n) - ay(n-1) = 0 \\ \frac{y(n)}{y(n-1)} = a$$

说明y(n)是一个公比为a的几何级数，所以：
$y(n) = Ca^{n}$
由特征方程我们知道：$r-a=0,r=a$

通常的，根据特征根，我们可以得到齐次解的三种情况：

1. 无重根：$y(n) = C_{1}(r_{1})^{n} + C_{2}(r_{2})^{n} + \dots +C_{n}(r_{n})^{n}$
2. 有k重根：$y(n) = C_{1}(r)^{n} + C_{2}n(r)^{n} + \dots C_{n}n^{k-1}(r)^{n}$
3. 有复数根：对于实系数的差分方程而言，如果出现复数根，那么此时必然是两个共轭的复数根。

假定特征根为：

$$r_{1} = Me^{jw} \\ r_{2} = Me^{-jw}$$

那么容易知道此时：

$$y(n) = C_{1}(r_{1})^{n} + C_{2}(r_{2})^{n} //将上面结果代入得到 y(n) = C_{1}M^{n}e^{jnw} + C_{2}(Me^{-jw})^{n}$$

再利用欧拉公式化简，并将任意常数合并后得到:$y(n) = PM^{n}\cos nw +QM \sin nw$.

特解

特解是依据激励的不同而得到不同的解，其与给定的激励信号有关，具体特解的形式可以参考如下列表：

奇异函数在离散系统下的响应

系统的因果性与稳定性

系统的因果性要求输出变化不领先于输入变化的系统，对于线性时不变系统是因果系统的充要条件。系统的稳定性则需要满足：$\sum_{n = -\infty}^{\infty} |h(n)| < \infty$.

单位样值响应绝对和为有限制，也称为绝对可和。

卷积和

卷积和的定义

任意序列x(n)可以表示为$\delta(n)$的加权位移的线性组合。同样的时不变性和均匀性、可加性也都满足。

离散卷积的性质

1. 交换律：x(n)h(n) = h(n) x(n)
2. 结合律： x(n) h_{1}(n) h_{2}(n) = x(n) [h_{1}(n) h_{2}(n)]
3. 分配律： x(n) [h_{1}(n) + h_{2}(n)] = x(n) h_{2}(n) + x(n)* h_{2}(n)
4. 和冲击序列卷积： x(n) * $\delta(n-m)$ = x(n-m)

卷积和的计算

解析式法

离散卷的解析式积需要确定积分的上下限，同时合理处理阶跃函数的取值范围。

图解法

图解法可以概括为：“对位相乘再相加。”

赏

谢谢你请我吃糖果