数字电路与逻辑设计--第二章--逻辑代数与数字电路

逻辑代数与数字电路

逻辑代数在1854年就产生了，在1854年George Boole证明了逻辑不仅仅是一个哲学问题也是一个数学问题。香农在1937年的硕士论文中提出了逻辑代数与数字电路之间的关系。实际上，逻辑代数是一种比数字电路更加本质的数学模型。

也就是说现阶段的半导体器件只是实现数字电路的一种手段，逻辑代数及其构建的数字系统是具有一种系统上的本质特征。

逻辑代数的三种基本运算

与或非

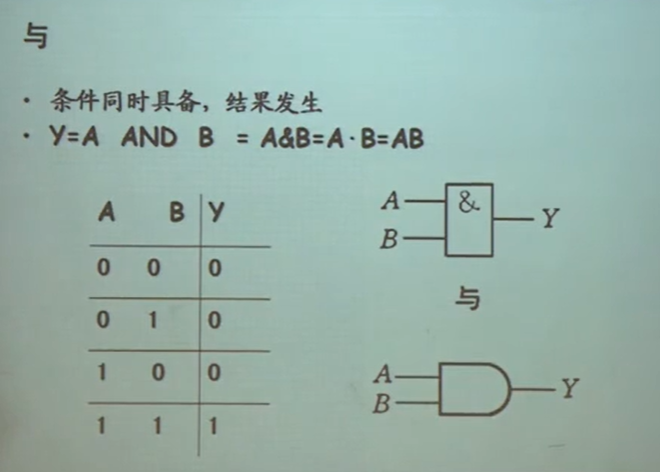
与

所谓与的关系就是说，条件同时具备的时候，结果发生，具体表示如下：

$$y= A AND B = A&B = A \cdot B =AB$$

对于两个变量的与关系，其真值表如下：

或

条件之一具备，则结果发生
y = A OR B = A+B

非

Y = A’ =NOT A

在逻辑电路图中，取反通过一个小圆圈表示，也就是说碰到类似的小圆圈图形就进行取反操作。

复杂逻辑

复杂逻辑分解到底层，本质就是与或非三种逻辑运算，也就是说上述三种逻辑构成了事实上的整体逻辑。

异或与同或

异或就是当运算的二者不同就取1，二者相同则取零。接下来我们来分析异或和与或非之间的关系。通过对逻辑代数的分析，我们容易知道,异或运算本质上也就是$\bar{A}B+A\bar{B}$.
而同时在异或基础上再整体取反就得到同或的表达式$\bar{\bar{A}B+A\bar{B}}$.

逻辑代数中的公式及其运算

基本公式

下表中给出了逻辑代数中的全部基本常用公式：

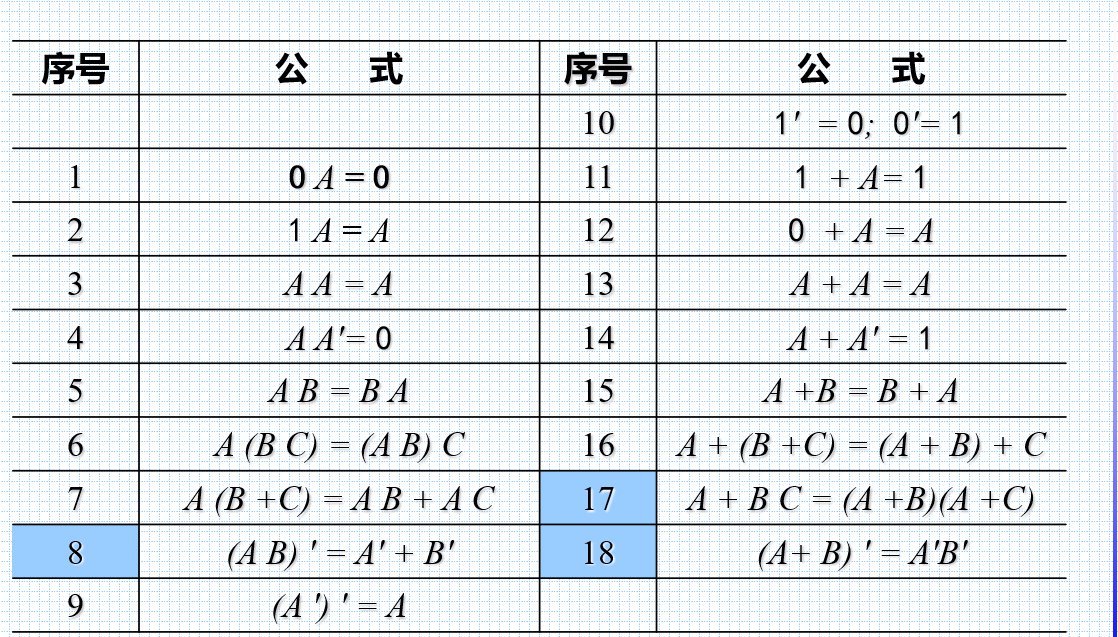
接下来对于其中重要的几条我们进行逐一介绍：
首先我们知道，对于逻辑代数而言，由于其取值确定，所以其必定能够通过真值表证明。接着来我们通过较为巧妙和数学化的推理得到几条重要公式的证明：

A+BC = (A+B)(A+C)

(A+B)(A+C)=A+AB+AC+BC=A(1+B+C)+BC=A+BC；证明完毕。

(AB)’ = A’+ B’

这个公式的证明设计到逻辑的本质，也就是二者同时取到的对面时二者中有一者不能取到。于是我们容易证明上述公式，

(A+B)’ = A’B’

这个公式的证明也需要考虑逻辑代数的本质，具体来说也就是A、B中任意发生一者的反面是AB两者均不发生，也就是说

上述两个公式实际上描述了与的对面是或，或的对面是与的逻辑本质。

常用公式

常用公式相比于基本公式更为复杂，但是实际上也是从基本公式推导得到的。

逻辑代数的基本定理

代入定理

在任何一个包含A的逻辑样式中，若以任何另外一个逻辑样式代入式中A的位置，那么等式依然成立。

上述定理实际上描述了数字电路模块化的根本思想。

反演定理

对于任何一个逻辑式，想要对其取反时，只需要将其与变为或，或变为与，0变为1，1变为0即可。实际上反演定理使用并不多，因为对于实际数字电路而言，取反只需要加一个反相器即可，并不需要手动进行新的逻辑推导。

逻辑函数及其表示方法

Y = F(A,B,C,…)

事实上，若以逻辑变量为输入，运算结果为输出，则输入变量确定之后，输出的取值也随之确定，那么输入/输出之间时一种函数关系。在二值逻辑中，输入、输出都只有两种取值，也就是0和1.

事实上逻辑函数有多种描述方法，可以采用真值表、逻辑式、逻辑图、波形图、卡诺图、EDA中的硬件描述语言等方法来描述。各种表示方式可以互相转换。

各种形式的表示方法

真值表

真值表是指的一种遍历当前输入和输出所有取值可能的表格，其能够完整表示一个逻辑函数，但是从逻辑抽象的层面而言，其抽象程度较低。

逻辑式

逻辑式指的是将输入于输出之间的逻辑关系使用与或非的运算式表示就得到的逻辑式。是在所有表示方法中最为数学化和抽象化的一种表达形式。

逻辑图

使用逻辑图形符号表示逻辑运算关系，于数字逻辑电路中的元器件相对应。使用这种方法表达逻辑函数能够帮助我们设计数字逻辑电路。

波形图

将输入变量所有可能的取值与对应输出按照时间顺序排列起来画成时间波形，这种逻辑函数的表达形式是我们在实验中最容易观察到的一种表达形式。

卡诺图

卡诺图是逻辑函数的一种图形表示方法，一个逻辑函数的卡诺图就是将此函数的最小项表达式中的最小项相应地填入一个方格图内，此方格图就成为卡诺图。卡诺图的构造特点具有一个重要性质：可以直观地从图上找出相邻的最小项，那么两个相邻的最小项可以合并为一个与项，同时消去一个变量。

EDA中的描述方式

EDA中存在多种多样的对逻辑函数的描述方法，其中常见的有如下几种：

1. HDL(Hardware Description Language),其中又以VHDL(Very High Speed Language)和Verilog Hdl 两种为主.
2. EDIF（Electronic Design Interchange Format），电子设计交换格式。EDIF综合了多种格式中的最佳特性，1985年的EDIF100版本提供了门阵列、半导体集成电路设计和布线自动化交换信息的格式，而后的EDIF200版本是不同EDA厂家之间交换设计数据的标准格式。
3. DTIF

各种表现形式的互相转换

真值表和逻辑式

我们以就判别函数的真值表为例，要求如下：
目前有三位二进制数，如果在此三位二进制数中含有偶数个1，那么此时为1，否则为0.对此容易绘制出真值表：

事实上，我们在写逻辑函数也就是在写真值表中为1的项，那么我们只需要找出其中为1的项，然后将其相或起来就行了，对于特定的相与的项，我们可以找出其中所有变量，如果该变量取1则此时逻辑函数中取其原变量，否则取其反变量。

对于上述真值表，我们可以转换如下：

$$A=0,B=1,C=1,使得A'BC=1 A=1,B=0,C=1,使得AB'C=1 A=1,B=1,C=0,使得ABC'=1$$

那么容易得到：$Y = A’BC + AB’C +ABC’$.

反之，从逻辑式到真值表更为简便，实际上就是简单的逻辑代数运算，首先写出有限个变量所有取值的可能，而后再将此时这些变量逐一代入到逻辑式中，得到相应输出量即为因变量的取值，

逻辑式与逻辑图

在器件充足的情况下，容易直接从逻辑式得到逻辑图，弱此时期间不足，则可能需要对逻辑式进行合理简化，其中使用最多的定理就是摩根定理。此外，对于实验中某些闲置的端，需要合理处理，例如对于与门闲置端口需要加1，对于或门，闲置端口需要加0.

懂逻辑图到逻辑是分析实际工程常用的方法，例如对于：

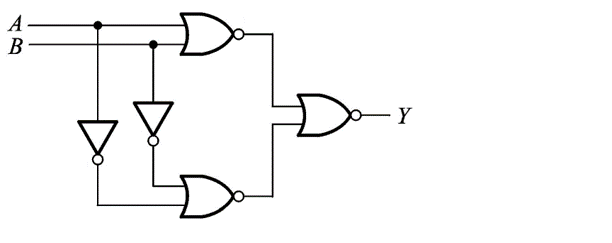
那么对于上述电路，我们可以做如下的化简：

$$((A+B)'+(A'+B')')'=(A+B)(A'+B')=AB'+A'B$$

事实上就将上述式子化为一个异或的表达式。

波形图到真值表

在波形图到真值表中需要注意的一个事宜是，取值一定要完整。

逻辑函数的两种标准形式

逻辑函数由于逻辑代数可以增加任意多个有限的变量，那么此时事实上对于逻辑函数的表达形式的不确定的，这种不确定性给我们带来了很多麻烦，对此我们对其规定了两种逻辑函数的标准形式：最小项之和和最大项之积。

最小项与最小项之和

最小项m：最小项m是乘机项，且其必须包含n各因子，n各变量均以原变量和反变量的形式在m中出现一次。对于n个变量的逻辑函数，会产生$2^{n}$个最小项，实际上也就是真值表上所有的取值可能。于是最小项之和恰好可以对应于真值表中为1的项。

对于这种最小项之和的编码方式，事实上对应于真值表中特定的一行，这种方式也就确保了真值表的唯一性。最小项由此也带来一些性质，有且仅有一个最小项的值为1，同时全体最小项之和也为1.
同时由于最小项取值的唯一性，那么可以知道任何两个最小项的积为0.
两个相邻的最小项之和可以合并，小区一对因子，只留下公共因子。所谓两个变量相邻，事实上也就是指的，两个最小项之间仅仅有一个变量不同。例如：$A’BC’和A’BC可以消去C：$.

$$A'BC'+A'BC = A'B(C+C')=A'B$$

最大项与最大项之积

最大项可以通过最小项通过摩根定理取反，那么如果此时对于某一最小项必然有唯一与其对应的最大项。最大项的本质对应着的是真值表中为0的一行。

最大项的标准定义如下:最大项(M)是相加项，包含n个因子，n个变量均以 原变量和反变量的形式再M中出现一次。对于两个变量而言其原值实际上代表的是0，取反后代表的是1.

逻辑函数的化简

逻辑函数的最简形式指的是数学上的最简形式，在电路设计层面上不存在最好的逻辑函数，也就是说，对于实际工程中特定的需求，应该采用特定的逻辑函数表达形式。

逻辑函数的最简形式

首先我们给出一个例子：

$$Y_{1} = ABC + B'C +ACD \\ Y_{2} = AC + B'C$$

通过式子1的如下推演，我们容易知道：

$$Y_{1} = ABC + B'C + ACD = (AB + B')C + ACD = (A+B')C + ACD = AC +B'C$$

于是实际上述两个式子是等价的，但是表达形式是不唯一的。

于是我们定义了某种意义上的最简，在此主要是最简与或。

最简与或

包含的乘积项数最少，每个乘积项的因子也最少，成为最简的与或逻辑式。

$$Y_{1} = ABC + B'C +ACD \\ Y_{2} = AC + B'C$$

用通俗的语言来解释就是相或的项要尽可能地少，且相或的项要尽可能地短。对于逻辑是的化简方法有很多种，接下来我们来逐一介绍。

化简方法

公式化简法

反复利用基本公式和常用公式，消除多余的乘积项和多余的因子，例如：

$$Y = AC + B'C +B'D +CD' + A(B+C') + A'BCD' + AB'DE$$

对于这个式子，首相考虑展开括号，那么得到：

$$Y = AC + B'C +B'D +CD' + AB+ AC' + A'BCD' + AB'DE$$

容易看出来，这个式子中含有：AC+AC’=A，那么一旦有A，凡是含有A的项则可以统统去掉。实际上公式化简法需要大量的经验累积。其意义是其解释了化简的基本规律，但是这个不是重点。

卡诺图化简法

卡诺图起源于逻辑函数的化简。将逻辑函数以最小项之和以图的方式表达出来，以$2^{n}$各小方块分别代表n变量的所有最小项，并将他们排列成举证，而且使集合位置相邻的两个最小项在逻辑上也是相邻的，也就是说此时只有一个变量不同，就得到表示n变量全部最小项的卡诺图。

也就是转逻辑上的相邻为几何上的相邻。卡诺图在绘制的时候时候是按照格雷码编排的。

使用卡诺图表示逻辑函数

1. 将函数表示为最小项之和的形式$\sum m_{i}$.
2. 在卡诺图上与这些最小项对应的位置添入1，其余位置填入0.（注意其是按照格雷码排列）

例如，对于以下四变量的逻辑函数：

合并原则，两个相邻的最小项可以消去一对因子，四个矩形的相邻最小项可以合并为一项，消去两对因子，同理八个相邻的最小项可以合并为一项，消去三对因子。

卡诺图化简步骤

1. 使用卡诺图表示逻辑函数
2. 找出可以合并的最小项
3. 化简后的乘积项可以相加，圈与圈之间可以重叠。

需要说明的是最简式不唯一，但是最简的逻辑代数式子中的相与项数唯一。画圈的时候需要注意，圈式可以重叠的，但是每个圈都需要有自己新鲜的1.

具有无关项数的逻辑函数及其化简

首先我们来介绍无关项，无关项分为两种，一种为约束项，一种为任意项。

1. 约束项：在逻辑函数中对输入函数取值的限制下，也就是在某些特定的条件下，不是所有的逻辑函数的取值均可以发生的。那么此时这些不可能发生的项就称为约束项。
2. 任意项：任意项意味着在某些情况下，某些变量的取值为1，或者为0均不一项逻辑函数取值的功能。

适合计算机的化简方法： Q-M法

1. 首先将逻辑函数化为最小项的形式
2. 将最小项进行编号，编号方式与通常情况不同，第一栏式不含有1的，第一栏的含有一个1的，第二栏式含有两个1的，以此类推
3. 那么此时不含有1和含有一个1；含有一个1和含有两个1的变量之间存在相邻关系。

赏

谢谢你请我吃糖果