引言
前面几章都是从分析学的角度来研究复变函数,本章将从几何的角度来研究复变函数,特别是解析函数的几何映射特征。具体地说z平面上的某一曲线,经过映射w=f(z)后在w平面上的像到底发生了什么变化。
共形映射的概念
伸缩率与旋转角
为了定量刻画映射前后图形之间的关系,我们引入伸缩率与旋转角两个概念。如图所示,过点$z_{0}$的曲线$C_{0}$经过$w=f(z)$映射后,变成了过$w_{0}$点的曲线$T^{0}$。容易看出,曲线发生了伸缩和旋转变换。
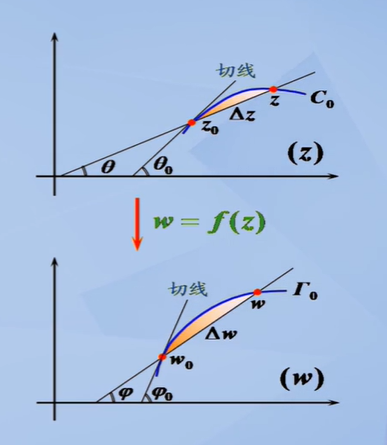
伸缩率
若极限$\lim_{z\to z_{0}}\frac{w-w_{0}}{z-z_{0}}=\lim_{\Delta z\to 0}\frac{\Delta w}{\Delta z}$存在,且,为曲线$C_{0}$经过$w=f(z)$映射后在$z_{0}$点的伸缩率。也就是我们将经过映射前后的模长之比定义为伸缩率。
旋转角
称$\lim_{z\to z_{0}}(\phi -\theta)=\phi_{0} - \theta_{0}$为曲线$C_{0}$经过$w=f(z)$映射后在$z_{0}$点的旋转角。
容易看出伸缩率和旋转角这两个概念刻画了曲线伸缩前后的局部变化特征。
导数的几何意义
设函数$w=f(z)$在区域D内解系,且有$z_{0}\in D$,且$f’(z_{0}) \neq 0$.于是按照导数定义,我们有如下表达式:
又由$\Delta w = |\Delta w|e^{i\phi},\Delta z=|\Delta z|e^{i\theta}$,有:
又因为导数可以按照如下形式表示:
共形映射的性质
- 导数的几何意义
$|f’(z_{0})|$事实上即表示曲线$C_{0}$在$z_{0}$点的伸缩率,而$arg f’(z_{0})$为曲线$C_{0}$在$z_{0}$处的旋转角。 - 不变性
不变性分为连个方面,一方面是伸缩率不变性,另外一方面是旋转角不变性。
于是我们知道任何一条经过$z_{0}$点的曲线的伸缩率均为$|f’(z_{0})|$,旋转角均为$arg f’(z)$. - 保角性
通过旋转角不变性,我们有如下性质$arg f’(z_{0}) = \phi_{0} - \theta_{0} = \phi_{1}-\theta_{1}$,于是我们可以推得:
也就是上述映射保持了两条曲线的交角的大小与方向不变。
第一类保角映射
通过上述分析,我们可以给出第一类保角映射的定义:
若函数w=f(z)在区域D内满足如下两个条件:
(1)保角性
(2)伸缩率不变性
于是我们称函数w=f(z)为区域D内的第一类保角映射。
于是我们容易知道,若函数w=f(z)在区域D内解系,且$f’(z) \neq 0$,则函数$w=f(z)$为区域D内的第一类保角映射。特别指出的是,导数不为0是必要的,否则会使得图形退化。
第二类保角映射
若函数w=f(z)在区域D内满足:
- 能保持两条曲线交角的大小不变,但方向相反
- 伸缩率不变性
那么我们则称函数w=f(z)为区域D内的第二类保角映射。
共形映射
若函数w=f(z)为区域内的第一类保角映射,且当$z_{1} \neq z_{2}$时,$f(z_{1}) \neq f(z_{2})$,则称$w=f(z)$为区域D内的共形映射。
也就是说除了要求映射是第一类保角映射外,还要求函数必须是双射。
共形映射的基本问题
共形映射研究的两个基本问题
共形映射研究的两个基本问题分别是:
- 对于给定的区域D和定义在区域D上的解析函数$w=f(z)$,求其像集合$G=f(D)$,并讨论f(z)是否将D共形地映射为G?
- 对于给定的区域D和G,求一解析函数w=f(z)使得f(x)能够将D共型映射为G.这一问题也称为共形映射的基本问题。
问题一有关定理定理介绍
保域性定理
设函数w=f(z)在区域D内解析,且恒不为常数,则其像集合G=f(D)仍然为区域。
边界对应原理
设区域D的边界为简单闭曲线C,函数w=f(z)在闭域$\bar{D}=D+C$上解析,且将曲线C双方胆汁地映射为简单闭区线$T$.那么当z沿着C的正向绕行时候,相应的w的绕行方向记为
上述定理将像区域的求解问题转化为像区域边界的求解问题,而对于边界曲线就可以转换为函数的研究。于是我们给出求解像区域的一般步骤。
求解像区域的一般步骤
设函数w=f(z)在闭域$\bar{D}=D+C$上解析,且为一一映射。
令z=x+iy, w=u+iv,则可以求得
求解边界曲线C的像T。也就是将A式代入曲线C的方程化简。
对于确定像区域边界曲线问题主要有两种解决方案方案:
- 在边界C的正向找三点,考察像点的走向
- 在区域D的内部找一点,考察像点的位置
此外针对具体的函数和区域,将还会有一些特殊的方法来解决有关问题。
问题二有关定理介绍
首先我们需要考虑此类映射是否存在,可由如下定理来解决
黎曼存在唯一性定理
- 设D和G是任给的两个单连域,在其各自的边界上至少含有两个点,则一定存在解析函数$w=f(z)$将区域D共形地映射为G。
- 如果在区域D和G内再分别指定一点$z_{0}$和$w_{0}$,并任意给定一个实数$\theta_{0} \in (-\pi,\pi]$,使得$arg f’(z_{0})=\theta_{0}$且$f(z_{0})=w_{0}$,则映射w=f(z)是唯一的。
问题的简化
对于给定的单连域D,求共享映射,使得D映射为单位圆域,事实上,由此即可求得 任意两个单连域之间的共形映射。
分式线性映射
分式线性映射的定义
有分式线性函数$w= \frac{az+b}{cz+d}$(a,b,c,d 均为复数,且$\frac{a}{c} \neq \frac{b}{d}$)构成的银蛇,称为分式线性映射,特别地,若c=0,则称为整式线性映射。
容易函数分式线性映射的复合依然是一个分式线性映射,分式线性映射的逆映射也是一个分式线性映射:$z= -\frac{dw-b}{cw-a}$.
简单函数的分式线性映射
平移映射
平移映射就是将点集沿着向量方向平移其模长的距离。
旋转映射
令$z=z|z|e^{i\theta}$,则有:$w=|z|e^{i(\theta + \theta_{0})}$,特点,旋转映射能够将点集绕原点旋转一个角度$\theta_{0}$.
具体来说,当$\theta_{0} >0$时,沿逆时针旋转,当$\theta_{0} <0$时,沿顺时针旋转。
相似映射
令$z=|z|e^{i\theta}$,则有$w=r|z|e^{i\theta}$.相似映射保持点的幅角不变,但模扩大(缩小)相应的r被,因此它将点集沿着极径方向相似得扩大或者缩小r倍。
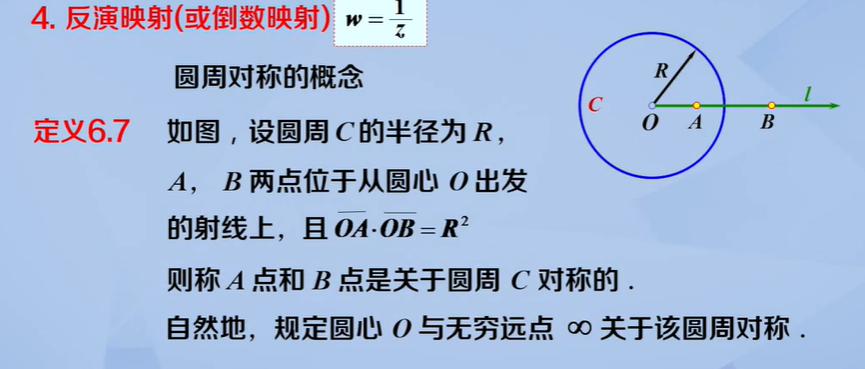
反演映射
令$z=|z|e^{i\theta}$,则有$w=\frac{1}{|z|}e^{i(-\theta)}$,他们的模互为倒数,且幅角反号。反演映射是将单位圆内的点映射到单位圆外,将单位圆外的的映射到单位圆内。
分式线性映射的特性
保形性
由于分式线性映射$w=\frac{az+b}{cz+d}$可分解为(整式)线性映射和倒数线性映射的复合。由于整式线性映射条件性质良好,下面我们主要讨论倒数映射$w=\frac{1}{z}$的性质。
单值性
规定: 当$z=\infty$时,w=0;当$z=0$时,$w=\infty$,由此可以看出导数映射在扩充复平面上是单值的。
解析性
- 当$z \neq \infty$且$z \neq 0$时,函数$w = \frac{1}{z}$解析,且$\frac{dw}{dz} = -\frac{1}{z^{2}}$不为0.
- 当$z=\infty$时,函数$w=\frac{1}{z}$,此时令$\epsilon = \frac{1}{z}$,则$w= \epsilon = \phi (\epsilon)$,函数$\phi (\epsilon)$在0处解析,且$\phi ‘(0)=1 \neq 0$.
通过上述分析可知,函数$w= \frac{1}{z}$在扩充复平面上除$z=0$外是共形映射。
于是通过如下变换容易得出倒数映射$w=\frac{1}{z}$在$z=0$处也是共形映射。说明如下:
已知$w=\frac{1}{z}$在扩充复平面上除了z=0外均是共形映射,那么$z = \frac{1}{w}$在w扩充复平面上除了w=0外均是共形映射。特别地$z=\frac{1}{w}$在$w=\infty$处是共形映射,由此可以得到$w=\frac{1}{z}$在$z=0$处是共形映射。
保圆性
倒数映射具有保圆性,有$w=\frac{1}{z}$可知,有$z=\frac{1}{w}$,令$z=x+iy,w=u+iv$,则有$x+iy = \frac{1}{u+iv} = \frac{u}{u^{2}+v^{2}}+i\frac{-v}{u^{2}+v^{2}}$.于是我们就得到了
将此关系带去平面上任意一个源,可以知道,此时任然得到一个圆。同时对于分式线性映射而言,我们有如下定理,在扩充复平面上,分式线性映射能够把圆变成圆,也就是分式线性映射具有保圆性。
对于保圆性的几点说明:
- 如果给定的圆(或者直线)上没有点映射为无穷远点,则他就映射为半径有限的圆。
- 若给定的圆或者直线上有一点映射为无穷远点,那么它就映射为直线。
- 若对于圆弧、或者直线,如果其中一个端点映射成无穷远点,则他就映射为射线。
保对称性
假若点$z_{1},z_{2}$关于圆周C对称,则在分式线性映射下,它们的像点$w_{1},w_{2}$也关于像曲线$C’$对称。
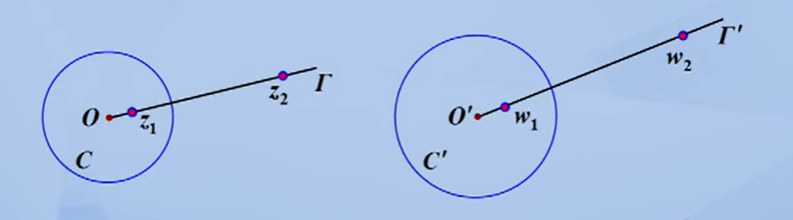
分式线性映射的分解
对于分式线性映射,主要有以下四种方法求得其在分式线性映射下的像曲线:
- 分解为四种简单映射的复合。
- 利用保圆性,取三点定圆,对于圆弧段或者直线段,两个端点必须选定。
- 综合利用保圆性和保角性,首先找出原像曲线中一些特殊点的对应的像点,从而大致地确定处曲线的位置,然后找出一些特殊的曲线所对应的像,最后通过原像之间的关系确定像之间的关系即可。
位移决定分式线性映射的条件
对于某分式线性映射
中含有四个常数a,b,c,d.实际上,通过分子分母同除某一常数将其归一化,容易知道,实际上分式线性映射中只存在三个独立的常数。由此可见需要给定三个条件,就能够决定一个分式线性映射。
于是有如下定理:在z平面上任意给三个不同的点$z_{1},z_{2},z_{3}$,在w平面上也任意给定三个不同的点$w_{1},w_{2},w_{3}$,那么此时存在 唯一的 分式线性映射,将$z_{1},z_{2},z_{3}$分别依次映射为$w_{1},w_{2},w_{3}$。
且此时该线性分式映射求解过程如下:
假定存在某一线性分式映射为$w = \frac{az+b}{cz+d}$.那么容易得到如下比值关系:
由上述比值化简后得到如下公式,我们称为对应点公式:
由于分式线性映射具有保圆性,因此该公式通常用于:把过$z_{1},z_{2},z_{3}$三点的圆或者圆弧映射到过$w_{1},w_{2},w_{3}$三点的圆或者圆弧,
同时若$z_{1,2,3},w_{1,2,3}$中任意一点为无穷远点,则需要在对应点公式中将其替换为1.
接下来我们做一个简要的说明:设$w=f(z)$为分式线性映射,且$f(z_{1})=w_{1},f(z_{2})=w_{2}$,那么上式可以表示为:
特别地,若$f(z_{1})=0,而f(z_{2})=\infty$,那么则有$w=k\frac{z-z_{1}}{z-z_{2}}$.
两个典型区域之间的映射
两个典型区域分别指的是上半平面和单位圆域,由于这通常映射均可以由此二者的映射转换推导出来。
上半平面映射为单位圆域
将上半平面映射为单位圆域有多种方法:
1, 三点定圆:在实轴和单位圆周上分别取三点:例如$z_{1}=0,z_{2}=1,z_{3}=\infty$和$w_{1}=-1,w_{2}=-i,w_{3}=1$.依据对应点公式即可得到此时$w=\frac{z-i}{z+i}$.
需要说明的是,此时对应并不是唯一的,当我们取点不同,得到的对应法则也不尽相同。所以需要依据不同的点来确定对应法则。
- 通用解法:在上半平面内任取一点$z_{0}$,使其映射到w平面的点$w_{1}=0$,依据保对称性,则有:
从而容易构造此时的分式线性映射为:
而当z在实轴上取值的时候,有
由此可以推知:
那么得到同式表达式:$w=e^{i\theta \frac{z-z_{0}}{z-\bar{z_{0}}}}$.
特别地,若取$\theta = 0,z_{0}=1$,那么此时得到了和方法1一样的结果。
单位圆域映射到单位圆域
首先我们给出一种能够直接求解通式的方法:
在|z|<1内任取一点$z_{0} \to w_{1}=0$,由保对称点性,知道$\frac{1}{\bar{z_{0}}} \to w_{2}=\infty$.因此相应的分式线性映射为:
也就是:
初等函数的映射
幂函数
幂函数$w=z^{n},(n \geq 2 为整数)$
令$z=re^{i\theta}$,那么此时有$w=r^{n}e^{in\theta}$,即$|w| = r^{n}$,$arg w =n \theta$.
幂函数的映射性质
幂函数映射的本质就是扩大顶点在原点的角形域(或扇形域).相应地,更是函数的映射特点就是缩小顶点处的角形域和扇形域。
幂函数的保形性
分析(1)在z平面上处处解析,且$\frac{dw}{dz} = nz^{n-1}$;显然只有当$z \neq 0$时幂函数的倒数不为0.于是我们容易知道,除了原点外,幂函数$w=z^{n}$是复平面上的第一类保角映射。同时若在角形域或者扇形域$(0 < \theta < \theta_{0})$上,如果$\theta_{0} \leq \frac{2\pi}{n}$,则幂函数$w=z^{n}$是共形映射。
指数函数
指数函数$z=x+iy$,则有$w=e^{z}=e^{x}\cdots e^{iy}$.

可以说指数函数$w=e^{z}$的映射特点就是将水平带形映射为复平面上的扇形或者圆。
