决策
什么是决策?
决策,顾名思义,做决定,做选择。决策是某一种决定,为了实现特定的目标,依据客观的可能,在占有一定信息和经验的基础上,借助一定的工具、技巧和相应方法,对当前情况做出判断,我们称为决策。而人类智能的一个重要标志就是能通过对当前环境情况的判断从而做出相应决策。
贝叶斯决策
贝叶斯决策的概念
一切不确定的因素都通过概率或者概率分布来表示,而后通过贝叶斯公式推理出目标的概率或者概率分布,最终做出决策。这种方法具有数学的逻辑性和严密性。接下来我们思考几个问题:在分类时我们是否必须计算概率?通过概率来描述不确定性因素是否合理?通过概率来做分类是否合理?
如何进行决策?
分类问题能不能避免分类错误?
如何减少错误?
不同错误造成的损失一样吗?
分类问题中物体的表示方法
假设一个待识别的物理对象用其d个属性观察值描述,称之为d个特征,记为$x=[x_{1},x_{2},x_{3},…,x_{d}]^{T}$.着组成一个d维向量,而这d维向量特征所有可能的取值范围则组成了一个d为的特征空间。所谓分类即使依据物体在特征空间中不同的位置进行对物体特性的划分。
分类问题的形式化定义如下:
已知:
- 总共由C个类别
- 每个类别的物体在这d维特征空间的统计分布,即类条件概率密度函数$P(x|w_{i})$,$w_{i}$表示第i个类别,其中i=1,2,3,…,C
- 每个类别物体发生的先验概率为$P(w_{i})$,i=1,2,3,…,C
决策问题
如何依据上述信息来判决输入样本x的所属类别。
最小错误率的贝叶斯决策
当某一特征向量x只为某一类所特有,即不可能出现分类错误。如下公式所表示:
但是不是所有样本都具有特定类别,像:天气预报、看病等等,对于同样的症状对于不同人具有不同的特征。也就是说很大程度上错误是不可避免的。同时需要指出的任何决策实际上由于种种不确定性因素都存在错判的可能性。于是为了使得错误率最小,就有了最小错误率贝叶斯决策方法。
最小错误率贝叶斯定义:
目标:判决错误的概率最小,于是我们成能够使得判决错误率最小的分类规则,我们就称之为最小错误率贝叶斯决策。
几个重要概率
在介绍贝叶斯决策之前,我们首先来了解几个重要的统计学概念。其中最重要的是如下三个概率的描述:
- 先验概率 $P(w_{i})$
- 类条件概率密度函数 $P(x|w_{i})$ (也称为似然函数)
- 后验概率 $P(w_{i}|x)$
接下来我们给出几个例子体会几个概率的含义:
先验概率
定义:先验概率是指根据以往经验和分析得到的概率,它往往作为,因果中的因。
作用与意义:在贝叶斯统计推断中,不确定数量的先验概率分布是在考虑一些因素之前表达对这一数量的置信程度的概率分布。
例如
异常细胞检测问题(新冠肺炎检测):
- $P(w_{1})和P(w_{2})$:每种细胞占全部细胞的比例在未查看样本情况下的概率类别估计。
- $P(w_{1})+P(w_{2})=1$,一把情况下正常细胞占比大。
对于上述问题描述,先验概率的得出是通过大量“实验”实践结果得出的,也就是说细胞检测的正常数据与异常数据的比值是在人类医疗科学经过大量实践后得到实践结论证明的。与此次样本数据没有必然的联系。但是作为一个有代表性的样本在大体上其概率分布应当复合先验概率。
接下来我们来对先验概率做一个说明:先验概率缺失提供了对分类有用的信息,但是先验概率是总体的一种估计,在实际具体分类问题中不具有使用价值,他也不能使得错误率达到最小。但是任然对分类问题提供了许多有用的信息,例如样本总体的分布。但是这种分类显然是不够准确,需要结合其他条件进一步使用。
类条件概率密度函数(似然函数)
定义:类条件概率密度是,假定x是一个连续随机变量,其分布取决于类别状态,表示成p(x|ω)的形式,而对应表示此关系的函数。
作用与意义:类条件概率密度函数描述了在已知某类别的特征空间中,出现特征值X的概率密度,
接下来我们依然使用上面的例子对类条件概率密度函数做一个解释:
例如:
在细胞检测中,通过对细胞做病理分析,得到正常类别$w_{1}$和异常类别$w_{2}$在d维观测空间中的分布特征,具体说来就是我们能求得当前各种细胞比例的人群所占总人群的具体比例。为例简单起见,我们假定只采用一个特征d=1.于是我们能够得到如下的两类概率密度函数分布:
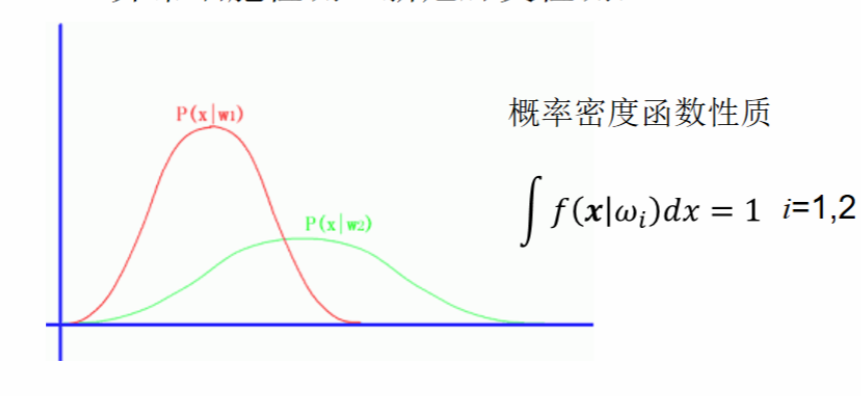
下面我们对类条件概率密度函数做一个简要说明:类条件概率密度函数在分类中是必须的,给我们提供了不同种类的特征分布。但是此方法没有考虑先验概率,也就是说没有考虑到样本内在的偏差。所以仅仅使用类条件概率密度函数来对样本进行分类也是不够准确的。
后验概率
定义:后验概率是指在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的”果”。先验概率与后验概率有不可分割的联系,后验概率的计算要以先验概率为基础。
后验概率的意义:事情还没有发生,要求这件事情发生的可能性的大小,是先验概率。事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是后验概率。先验概率不是根据有关自然状态的全部资料测定的,而只是利用现有的材料(主要是历史资料)计算的;后验概率使用了有关自然状态更加全面的资料,既有先验概率资料,也有补充资料,而补充资料大部分就是我们所说的类条件概率密度函数。
任然使用上述细胞检测例子做说明:
$P(w_{1}|x):$当观测向量为x值时,该细胞属于正常细胞的概率。
$P(w_{2}|x):$当观测向量为x值时,该细胞属于异常细胞的概率。
也就是考虑了当前观测结果与经验特征下得到的结论。
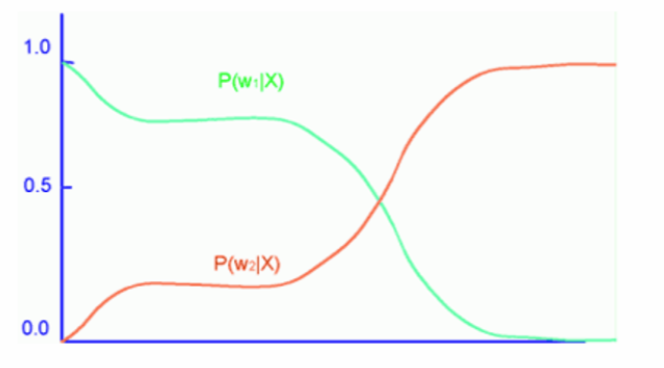
所有后验概率之和应当为1.
我们分析以下类条件概率密度函数和后验概率之间的区别:
此两者都是条件概率,但是后验概率是以当前样本观测数据作为条件求得的概率;而类条件概率密度函数是在不条件下讨论问题,得到的概率,其和也不为1.
贝叶斯公式
贝叶斯公式是概率论中一个十分重要的公式,在人工智能的实际应用中也具有不可替代的重要作用,它链接了先验概率、后验概率、类条件概率密度函数三者:
也就是依据先验概率和概率密度函数我们可以求得后验概率。
最小错误率与贝叶斯决策:
后验概率与错误率的联系
假设是一个二分类问题,那么后验概率与错误率之间存在如下关系:
- $P(w_{1}|x)$:样本x属于$w_{1}$的概率。
- $P(w_{2}|x)$:样本x属于$w_{2}$的概率。
如果上述情况发生错判也就是:
错误率=样本x不属于$w_{1}$的概率=$1-P(w_{1}|x)=p(w_{2}|x)$
为了减小错误率我们比较两个后验概率的大小,选择其中较大的即可。
贝叶斯决策理论方法的范式
贝叶斯决策理论所讨论的问题
已知:共有C类物体,以及先验概率$P(w_{i})$以及类条件概率密度函数$p(x|w_{i})$.
问题:如何对某一样本进行分类
通过最小错误率贝叶斯决策:通过贝叶斯公式计算出后验概率$P(w_{i}|x)$:
- 如果$P(w_{1}|x) > P(w_{2}|x)$,则我们将x归为$w_{1}$类别。
- 如果$P(w_{1}|x) \leq P(w_{2}|x)$,则我们将x归为$w_{2}$类别。
(实际上就是哪个后验概率大就把样本归入哪个类别。)
最小错误率贝叶斯决策的几种等价形式
后验概率形式:
先验概率以及条件概率密度函数表示:
比值形式:
对数似然比:
最小风险贝叶斯决策
概念
损失函数
